샤워를 하던 중 뜬금없이 ‘코사인 유사도 수식이 뭐였지?’ 하는 생각이 들었다.

기억 상 \(v \cdot w \over{\lVert v \rVert \lVert w \rVert}\) 로 (수식이 깨진다면 클릭)

내적을 통해 두 벡터의 유사도를 파악할 때 벡터 별 스케일 차이에 의한 판단의 어려움을

\(\lVert v \rVert \lVert w \rVert\) 를 통해 제거해준 것으로 알고 있었다.

이어서 피어슨 상관 계수와 수식이 매우 유사하다는 생각이 들었는데,

이참에 둘의 공통점이 무엇이고 차이점이 무엇인지 정리해보았다.

공분산과 피어슨 상관 계수

피어슨 상관 계수가 무엇인지 파악하기 위해 공분산이 무엇인지 알면 도움이 된다.

공분산을 통해 두 변수의 선형 관계를 파악할 때 평균과 표준편차가 달라 두 변수 간 관계가 얼마나 강한 것인지 판단할 때 어려움이 생기는데

이러한 어려움을 해소해준 것이 피어슨 상관 계수이기 때문이다.

공분산 수식은 다음과 같다. \[\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{n-1}\]

(공분산, 위키백과)

분자를 보면 \(X\)와 \(Y\) 라는 변수가 있을 때, \(X\)의 각 원소와 \(X\)의 평균을 뺀 값과 \(Y\)의 각 원소와 \(Y\)의 평균을 뺀 값을 곱하는 것을 알 수 있다.

\(X_{i}-\bar{X}\), \(Y_{i}-\bar{Y}\) 쌍이 서로 양의 값을 갖거나, 서로 음의 값을 갖는 경우가 많을수록 결과는 큰 양수가 될 것이고

\(X_{i}-\bar{X}\), \(Y_{i}-\bar{Y}\) 쌍의 부호가 서로 다를 경우 음수가 더해지기 때문에 이런 경우 결과는 음수가 될 것이다.

즉, 공분산은 \(\bar{X}\) 와 \(\bar{Y}\) 로 좌표평면을 나눴을 때 데이터 포인트가 1, 3 사분면에 많을 땐 양수, 2, 4 사분면에 많을 땐 음수가 나오게 된다. 따라서 두 변수가 양의 선형 관계를 나타낼 때 공분산은 양수, 음의 선형 관계를 나타낼 때 공분산은 음수이다.

다음 예시를 보자.

import numpy as np
import matplotlib.pyplot as plt


np.random.seed(500)
X = np.random.randint(10, 90, 500)
Y = X + np.random.normal(3, 7, 500)
x_mean, y_mean = X.mean(), Y.mean()

fig, ax = plt.subplots(figsize=(7, 7))
ax.set_aspect(1)

ax.axvline(x_mean, color='gray', linestyle='--')
ax.axhline(y_mean, color='gray', linestyle='--')

ax.scatter(
    X, Y,
    alpha=0.5,
    color=['royalblue' if (x>x_mean and y>y_mean) or (x<x_mean and y<y_mean) else 'gray' for x, y in zip(X, Y)],
    zorder=10,
)

ax.set_xlabel('$x$')
ax.set_ylabel('$y$')

ax.set_xlim(-3, 103)
ax.set_ylim(-3, 103)
plt.show()

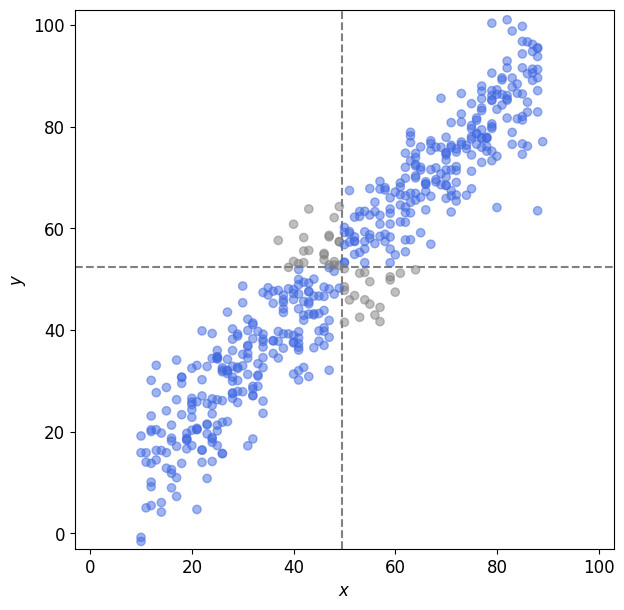
임의로 0 ~ 100 사이 값을 갖는 \(X\), \(Y\) 변수로 그린 산점도다. 회색 점선은 각각 \(\bar{X}\), \(\bar{Y}\) 를 나타낸다.

위 산점도의 파란색 데이터는 공분산이 커지는 데 기여하고 회색 데이터는 공분산이 작아지는 데 기여한다.

얼핏 보아도 파란색 데이터가 훨씬 많고 평균선과도 멀리 떨어져 있는 포인트가 많다. 공분산 값이 꽤 클 것이다.

def get_covariance(X, Y):
    assert X.ndim == 1 and Y.ndim == 1, "X and Y must have a 1dim"
    assert len(X) == len(Y), "X and Y must be the same length"
    return ( ( X - X.mean() ) * ( Y - Y.mean() ) ).sum() / (len(X) - 1)

get_covariance(X, Y)

502.9611128715084

기대했던 것과 같이 공분산이 커다란 양수임을 알 수 있다.

공분산을 통해 두 변수의 선형 관계는 파악할 수 있지만 선형 관계가 얼마나 강한지 판단하기는 어렵다. 변수의 스케일에 따라 값이 달라지기 때문이다.

다음 예시를 보자.

X, Y = X / 10, Y / 10
x_mean, y_mean = X.mean(), Y.mean()

fig, ax = plt.subplots(figsize=(7, 7))
ax.set_aspect(1)

ax.axvline(x_mean, color='gray', linestyle='--')
ax.axhline(y_mean, color='gray', linestyle='--')

ax.scatter(
    X, Y,
    alpha=0.5,
    color=['royalblue' if (x>x_mean and y>y_mean) or (x<x_mean and y<y_mean) else 'gray' for x, y in zip(X, Y)],
    zorder=10,
)

ax.set_xlabel('$x$')
ax.set_ylabel('$y$')

ax.set_xlim(-3 / 10, 103 / 10)
ax.set_ylim(-3 / 10, 103 / 10)
plt.show()

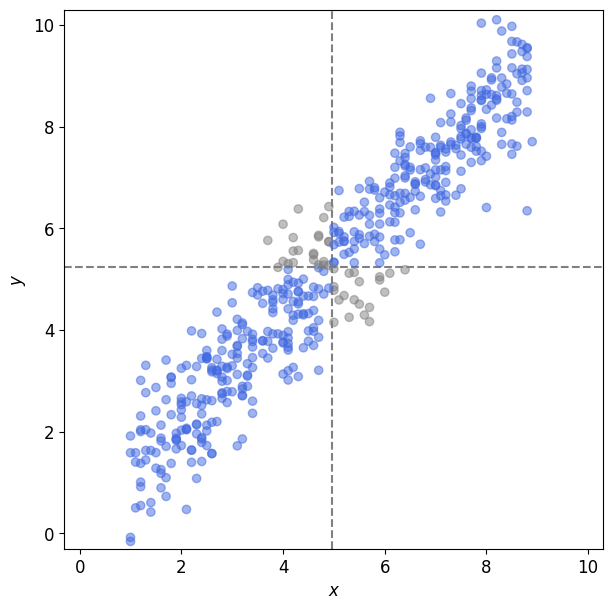
get_covariance(X, Y)

5.029611128715083

위에서 활용한 예시와 동일한 데이터에 대해 스케일만 1/10로 줄인 결과이다.

선형 관계의 강도는 동일하지만 공분산 결과는 1/100 만큼 차이가 난다.

이처럼 공분산을 통해 선형 관계의 강도가 얼마나 강한지는 판단하기 어려운데, 이러한 공분산의 단점을 해소해주는 것이 피어슨 상관 계수이다.

피어슨 상관 계수 수식은 다음과 같다. \[\frac{\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{n-1}}{\sqrt{\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)^{2}}{n-1}} \sqrt{\frac{\sum_{i}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}{n-1}}} = \frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}\]

(피어슨 상관 계수, 위키백과)

두 변수의 공분산을 각각의 표준 편차의 곱으로 나눈 것으로 \(X\) 와 \(Y\) 변수의 분산이 1로 조정돼 스케일에 따른 효과가 사라진다.

수식으로 좀더 살펴보자.

\({\sqrt{\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)^{2}}{n-1}}} = \sigma_X, {\sqrt{\frac{\sum_{i}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}{n-1}}} = \sigma_Y\) 이면, \[\frac{\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{n-1}}{\sqrt{\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)^{2}}{n-1}} \sqrt{\frac{\sum_{i}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}{n-1}}}\]

\[= \frac{\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{n-1}}{\sigma_X \sigma_Y}\]

\[= \frac{1}{n-1} \sum_{i}^{n}\frac{\left(X_{i}-\bar{X}\right)}{\sigma_X} \frac{\left(Y_{i}-\bar{Y}\right)}{\sigma_Y}\]

위와 같이 각 변수에 대해 표준화하고 공분산을 계산한 것과 동일하기 때문에 피어슨 상관 계수의 결과는 변수의 스케일에 상관없이 -1 ~ 1 사이 값을 갖게 된다.

이렇듯 피어슨 상관 계수를 통해 공분산으로 불가능했던 두 변수 간 선형 관계의 강도를 비교할 수 있다.

앞서 본 예시 \(X\), \(Y\) 변수로 확인해보자.

def get_pearson_correlation(X, Y):
    assert X.ndim == 1 and Y.ndim == 1, "X and Y must have a 1dim"
    assert len(X) == len(Y), "X and Y must be the same length"

    sigma_x = np.sqrt( ( (X - X.mean()) ** 2 ).sum() / (len(X) - 1) )
    sigma_y = np.sqrt( ( (Y - Y.mean()) ** 2 ).sum() / (len(Y) - 1) )
    return get_covariance(X, Y) / ( sigma_x * sigma_y )

print(f"공분산: {get_covariance(X, Y):.4f} != {get_covariance(X * 10, Y * 10):.4f}")
print(f"피어슨 상관 계수: {get_pearson_correlation(X, Y):.4f} == {get_pearson_correlation(X * 10, Y * 10):.4f}")

공분산: 5.0296 != 502.9611
피어슨 상관 계수: 0.9523 == 0.9523

스케일의 차이로 공분산은 다르지만, 피어슨 상관 계수는 같음을 알 수 있다.

코사인 유사도

코사인 유사도는 두 벡터 간 유사도를 확인할 때 자주 쓰인다.

두 개의 벡터가 있을 때, 벡터의 크기와 관계없이 벡터의 방향이 얼마나 비슷한지 확인하여 유사도를 판단하는 방법이다.

수식은 다음과 같다. \[\frac{A \cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^{n} A_{i} \times B_{i}}{\sqrt{\sum_{i=1}^{n}\left(A_{i}\right)^{2}} \times \sqrt{\sum_{i=1}^{n}\left(B_{i}\right)^{2}}}\]

(코사인 유사도, 위키백과)

분자는 두 벡터의 내적이다. 앞서 공분산에서 확인한 것처럼, 두 벡터의 쌍(\((a_1, b_1), (a_2, b_2), ...\))이 서로 양수거나 음수일 땐 값이 커지도록 유도되고, 두 벡터 쌍이 서로 다른 부호를 가질 땐 값이 작아지도록 유도된다.

분모는 각 벡터의 L2 norm의 곱으로, 벡터 별 길이를 1로 조정해준다. 피어슨 상관 계수에서 각 변수의 표준편차를 통해 각 변수 별 분산을 1로 조정해준 것과 유사하다.

각 \(A\), \(B\) 벡터를 어떠한 변수를 의미한다고 생각해보면, 앞서 확인한 피어슨 상관 계수와 비교했을 때 변수 별 평균을 0으로 조정해주지 않는다는 점을 제외하고 똑같다.

코드로 확인해보자.

def get_cossim(X, Y):
    return X.dot(Y) / (np.sqrt((X ** 2).sum()) * np.sqrt((Y ** 2).sum()))

print(f"코사인 유사도: {get_cossim(X, Y):.4F}")
print(f"피어슨 상관 계수: {get_pearson_correlation(X, Y):.4F}")
print(f"평균(0) 조정, 코사인 유사도: {get_cossim(X - X.mean(), Y - Y.mean()):.4f}")

코사인 유사도: 0.9919
피어슨 상관 계수: 0.9523
평균(0) 조정, 코사인 유사도: 0.9523

수식을 통해 확인한 것처럼 \(A\), \(B\) 벡터의 평균을 0으로 조정하지 않는다는 점만 제외하면 코사인 유사도와 피어슨 상관 계수가 같다.

벡터의 유사성을 확인하는 것과 변수 간 선형 관계를 파악하는 것 사이에 꽤나 공통점이 있는 것 같다.

앞서 공분산과 피어슨 상관 계수를 확인한 산점도를 떠올려보면

코사인 유사도를 통해 500 차원의 벡터 두 개의 유사도를 보는 것은

벡터 별 평균을 의미하는 점선을 원점으로 옮긴 후, 각 벡터 원소들 사이 선형 관계의 강도를 통해 알아보는 것으로 생각할 수 있을 것 같다.

두 변수의 선형 관계가 강하다면 직관적으로 유사도도 높을 것이라고 기대하게 되는 것처럼

코사인 유사도와 피어슨 상관 계수는 매우 닮아있다.